BNN: il modello matematico che “anticipa” la neurodegenerazione

Un modello matematico-computazionale interpreta la neurodegenerazione come transizione di fase nelle reti cerebrali, legando perdita sinaptica, infiammazione e aggregazione proteica a instabilità e aumento di entropia.

Integrato con AI e apprendimento non supervisionato, il framework punta a prevedere segnali precoci e costruire curve di rischio individuali utili a medicina predittiva e digital twin.

Perché le patologie neurodegenerative chiedono un cambio di paradigma: dal racconto ai modelli predittivi

Le patologie neurodegenerative rappresentano una delle più complesse e sfuggenti sfide della medicina contemporanea. Esse comprendono un insieme di malattie caratterizzate da una progressiva e irreversibile perdita di struttura e funzione dei neuroni, culminante in un deterioramento cognitivo e motorio di gravità crescente. Tra le più note vi sono la malattia di Alzheimer, il morbo di Parkinson, la sclerosi laterale amiotrofica (SLA), la demenza frontotemporale e la malattia di Huntington.

Pur diverse per eziologia e manifestazioni cliniche, tali patologie condividono un denominatore comune: un progressivo disfacimento dei circuiti neuronali e delle reti sinaptiche che sostengono la funzione cognitiva e motoria.

L’estrema complessità del sistema nervoso centrale — con i suoi circa 86 miliardi di neuroni e oltre 10¹⁴ connessioni sinaptiche — rende insufficiente qualsiasi approccio puramente descrittivo. In questo contesto, la matematica emerge come linguaggio privilegiato per tradurre la complessità biologica in modelli formali capaci di catturare i principi dinamici alla base del funzionamento e della degenerazione neuronale.

Le patologie neurodegenerative impongono un livello ulteriore di complessità rispetto alla normale modellizzazione neurofisiologica. Il deterioramento progressivo delle connessioni sinaptiche, la perdita di plasticità, la disgregazione dei pattern di attivazione e l’aumento dell’entropia funzionale non sono soltanto fenomeni biologici: possono essere espressi come transizioni di fase dinamiche all’interno di un sistema complesso non lineare. In fisica, una transizione di fase è il passaggio improvviso di un sistema da uno stato a un altro (come l’acqua che ghiaccia a 0°C). Il nostro modello mostra che il cervello può comportarsi in modo analogo: funziona normalmente fino a una certa soglia, poi “transita” rapidamente verso uno stato di disfunzione. Questo spiega perché molti pazienti sembrano stabili per anni e poi declinano rapidamente.

L’obiettivo di questo lavoro è proporre una cornice teorica in cui la matematica diventi strumento diagnostico e predittivo. Attraverso l’uso combinato di equazioni differenziali, teoria dei grafi, analisi spettrale e modelli stocastici, si intende rappresentare l’evoluzione temporale delle reti neuronali durante il processo degenerativo.

Tali strumenti consentono non solo di descrivere il fenomeno patologico, ma anche di individuare possibili indicatori precoci del deterioramento — una sorta di “biomarcatori matematici” capaci di anticipare l’evidenza clinica.

Strumenti matematici fondamentali

La complessità delle patologie neurodegenerative richiede una descrizione che vada oltre la semplice analisi statistica dei dati clinici o neurofisiologici. Tali fenomeni implicano dinamiche temporali e strutturali che si manifestano su molteplici scale — dal livello ionico a quello delle reti corticali — e che possono essere comprese solo attraverso strumenti matematici capaci di catturare la loro natura intrinsecamente non lineare, adattiva e stocastica.

Equazioni differenziali e sistemi dinamici

Il decadimento funzionale di un circuito neuronale non è immediato ma progressivo. Per descriverne la velocità nel tempo, si utilizzano i sistemi di equazioni differenziali. Queste equazioni sono essenziali per modellare come la matrice di connettività C — che rappresenta la forza delle sinapsi — cambia continuamente sotto l’effetto della stimolazione neuronale e del danno cellulare.

Un’equazione differenziale descrive come una quantità varia nel tempo. Nel nostro caso, descriviamo come la forza delle connessioni cerebrali cambia istante per istante, in funzione di quanto il cervello le usa (plasticità) e di quanto si deteriorano (degenerazione).

Un modello generale di decadimento sinaptico può essere espresso come:

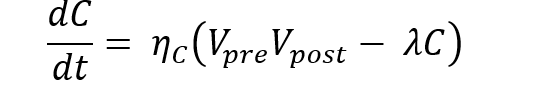
dove:

• C rappresenta la matrice di connettività sinaptica (quanto sono “forti” i collegamenti tra neuroni)
• V_pre e V_post indicano i vettori di attivazione pre- e post-sinaptici (quanto sono attivi i neuroni prima e dopo la sinapsi)
• η_C è il coefficiente di plasticità sinaptica (la capacità del cervello di rafforzare le connessioni usate)
• λ esprime il tasso di decadimento neuronale (la velocità con cui le connessioni si deteriorano)

Questa formula indica che la variazione di connettività (dC/dt) è la differenza tra Plasticità — la tendenza delle sinapsi ad attivarsi e rafforzarsi reciprocamente — e Degenerazione — il tasso di decadimento che riduce la connettività esistente, modellando l’effetto di accumulo proteico o stress ossidativo.

Quando λ supera un valore soglia λ_c, la rete non è più in grado di mantenere la coerenza funzionale e collassa in uno stato di frammentazione. Questo è il punto di non ritorno del sistema.

2.2 Teoria dei grafi e connettività cerebrale

Il cervello umano può essere rappresentato come un grafo G(V,E), dove i nodi V corrispondono ai neuroni o alle regioni corticali e gli archi E rappresentano le connessioni sinaptiche.

Un grafo è una struttura matematica composta da “nodi” (punti) collegati da “archi” (linee). È lo stesso modello usato per rappresentare le reti sociali (persone collegate da amicizie), le reti stradali (città collegate da autostrade) o internet (computer collegati da cavi). Il cervello è una rete biologica: i neuroni sono i nodi, le sinapsi sono gli archi.

Nelle patologie neurodegenerative, la topologia di questa rete si modifica nel tempo a causa della perdita di connessioni funzionali e strutturali, portando a una progressiva frammentazione del grafo cerebrale. Le metriche fondamentali per analizzare tale fenomeno includono:

• Grado medio |k|: misura la connettività media del sistema — quante connessioni ha in media ciascun neurone. La sua riduzione indica perdita di densità sinaptica.
• Coefficiente di clustering C: misura la tendenza dei nodi a formare gruppi funzionali locali — se i “vicini” di un neurone sono anche connessi tra loro. Nelle patologie degenerative tende a diminuire.
• Lunghezza media del cammino L: rappresenta la distanza media tra due nodi — quanti “salti” servono per andare da un neurone a un altro. Il suo aumento segnala un deterioramento della comunicazione neurale.
• Efficienza globale E_g: indica la capacità di integrazione e comunicazione veloce tra regioni cerebrali. Il calo di E_g è un segno di declino cognitivo.

2.3 Analisi spettrale e teoria delle matrici

Le proprietà dinamiche e di stabilità di una rete neuronale degenerante possono essere studiate attraverso l’analisi spettrale della matrice di adiacenza o di connettività A.

Gli autovalori (λ_i) di A rappresentano le modalità di oscillazione e sincronizzazione della rete. Il massimo autovalore λ_max è un indicatore di stabilità: quando scende al di sotto di una soglia critica λ_c, la rete entra in uno stato di de-sincronizzazione funzionale — perde la capacità di mantenere la sincronizzazione tra aree cerebrali.

La distribuzione di tutti gli autovalori permette di calcolare l’Entropia Cerebrale (S):

con

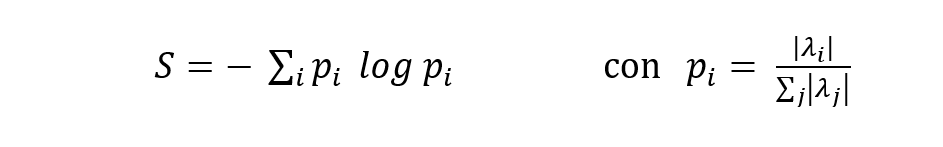
L’entropia è una misura del disordine. Un cristallo perfetto ha entropia bassa (tutto è ordinato); un gas ha entropia alta (le molecole si muovono caoticamente). Il cervello sano è in un equilibrio: né troppo ordinato (rigido) né troppo caotico (rumoroso). Nelle malattie neurodegenerative, l’entropia aumenta: il cervello diventa progressivamente più disorganizzato, come un’orchestra che perde il direttore.

Un aumento dell’entropia S corrisponde a una maggiore disorganizzazione delle connessioni neurali, coerente con quanto osservato nelle immagini di functional connectivity MRI (fMRI) nei pazienti affetti da Alzheimer o Parkinson.

Modelli stocastici e processi di diffusione

La degenerazione neuronale non è un processo deterministico ma stocastico: l’interazione tra fattori genetici, metabolici e ambientali introduce una componente di rumore biologico che può essere modellata mediante processi di diffusione o catene di Markov.

Un processo stocastico contiene una componente casuale, imprevedibile. La degenerazione cerebrale non segue un percorso identico in ogni paziente: ci sono fluttuazioni, variazioni individuali, eventi casuali (un’infezione, uno stress, un cambiamento metabolico) che influenzano la traiettoria. Il nostro modello incorpora questa variabilità attraverso un termine di “rumore”.

L’analisi della varianza del processo consente di identificare le fasi precoci del decadimento, in cui la variabilità aumenta prima della perdita strutturale definitiva — fenomeno noto come critical slowing down, tipico delle transizioni nei sistemi complessi.

Modellizzazione computazionale

La rappresentazione matematica delle patologie neurodegenerative acquista pieno significato quando viene tradotta in modelli computazionali capaci di riprodurre, in forma simulata, l’evoluzione dinamica della rete neuronale.

Il grafo sinaptico dinamico

Il cervello può essere rappresentato come un grafo dinamico G(V, E, t), in cui l’insieme degli archi E(t) varia nel tempo e ciascun arco è associato a un peso sinaptico C_ij(t), che rappresenta la forza di trasmissione tra due neuroni.

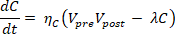
La prima parte dell’equazione (η_CV_iV_j) descrive l’apprendimento hebbiano — il principio per cui “neuroni che si attivano insieme, si rafforzano insieme”.

La seconda parte (−λC_ij) introduce il processo patologico di decadimento sinaptico.

Plasticità compensativa e ridondanza funzionale

Un aspetto osservato nei soggetti affetti da patologie neurodegenerative è la presenza di meccanismi di compensazione funzionale, in cui regioni non danneggiate assumono parzialmente il ruolo di quelle compromesse.

Questo fenomeno viene modellato introducendo un termine di plasticità compensativa ρ, che rappresenta la creazione di connessioni indirette o percorsi alternativi che la rete attiva per mantenere la funzionalità.

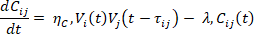
La riserva cognitiva spiega perché persone con lo stesso danno cerebrale (visibile alla risonanza) possono avere sintomi molto diversi. Alcuni cervelli sono più “resilienti”: hanno più connessioni ridondanti, più capacità di trovare percorsi alternativi. Il parametro ρ del nostro modello cattura matematicamente questa capacità di compensazione.

Questo termine introduce una non linearità che rende il sistema capace di mostrare fenomeni di auto-organizzazione parziale tipici delle fasi precoci di Alzheimer o Parkinson, in cui si osservano picchi transitori di attività compensativa prima del collasso definitivo.

Simulazioni e risultati

La simulazione permette di osservare curve di decadimento non lineare, caratterizzate da una fase iniziale di stabilità, seguita da un punto di biforcazione oltre il quale il sistema collassa rapidamente.

Poiché le patologie neurodegenerative presentano una forte eterogeneità clinica, è utile introdurre un approccio probabilistico basato su simulazioni Monte Carlo, in cui i parametri del modello (λ, η_C, ρ) sono distribuiti secondo leggi statistiche che rappresentano la variabilità biologica individuale.

Interpretazione biologica dei risultati

Il valore scientifico del modello risiede nella sua capacità di rappresentare fenomeni biologici reali. Ogni parametro matematico trova un corrispettivo osservabile:

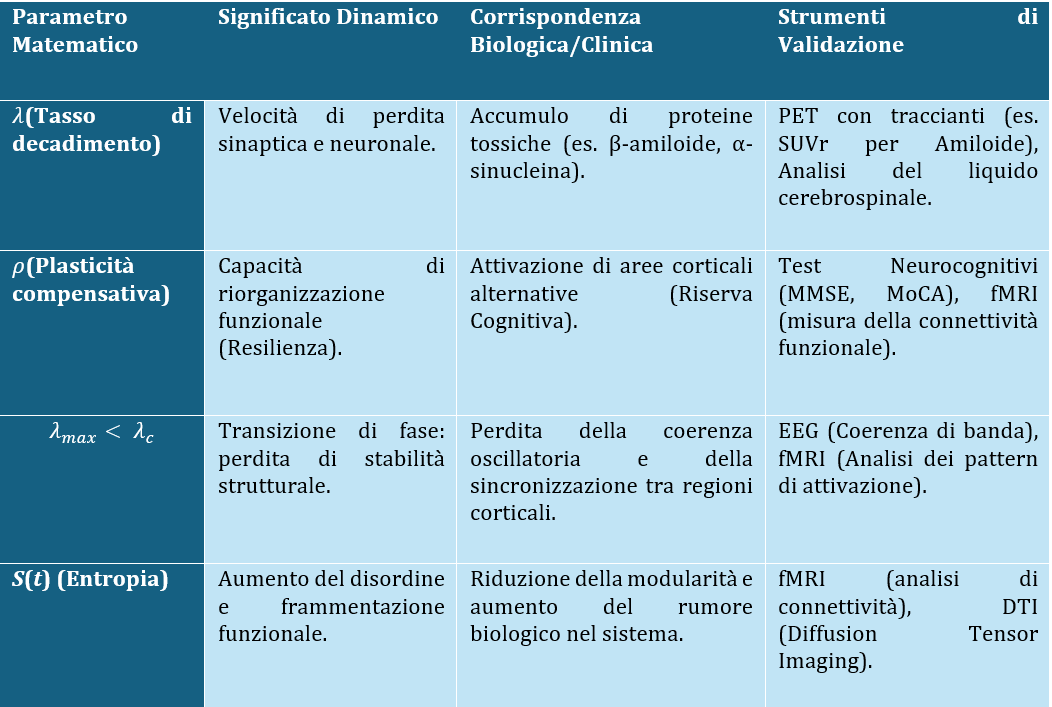
Il parametro λ può essere correlato direttamente ai valori di SUVr nelle PET con traccianti β-amiloide. L’entropia S(t) mostra correlazione con gli indici di connettività funzionale fMRI. Queste corrispondenze confermano la validità fisiopatologica del modello.

Verso un modello predittivo

L’obiettivo ultimo della modellizzazione dinamica non è solo descrivere lo stato delle cose, ma prevederne lo sviluppo futuro. I sistemi complessi, prima di un collasso strutturale, mostrano segnali di allarme precoce (Early Warning Signals) che la matematica può identificare molto prima dei sintomi clinici.

Critical slowing down

In prossimità del collasso (quando λ_max < λ_c), il cervello impiega molto più tempo a ritornare allo stato di equilibrio dopo una perturbazione. Questo fenomeno è noto come critical slowing down.

Matematicamente, si manifesta come:

• Aumento della varianza delle fluttuazioni neuronali
• Aumento dell’autocorrelazione temporale del segnale cerebrale

Identificare questi early warning permette di calcolare una soglia critica predittiva, che genera un allarme clinico personalizzato fornendo una finestra temporale cruciale per l’intervento terapeutico.

Architettura del modello predittivo ibrido

La costruzione di un modello predittivo affidabile richiede l’integrazione di approcci diversi. La nostra architettura ibrida si fonda su tre livelli interconnessi:

Livello 1 — Modello dinamico-matematico: produce la simulazione temporale dei parametri secondo le equazioni definite. Non si limita a descrivere i dati osservati, ma genera una rappresentazione causale del fenomeno.

Livello 2 — Apprendimento non supervisionato: utilizza tecniche come PCA e clustering per identificare pattern nascosti e raggruppare i pazienti in base alla loro traiettoria degenerativa.

Livello 3 — Rete neurale ricorrente (RNN): specializzata nell’analisi di sequenze temporali, viene addestrata a prevedere la probabilità di raggiungere il punto di non ritorno in una finestra temporale futura.

Le reti neurali artificiali tradizionali sono potenti ma “cieche”: imparano correlazioni statistiche senza capire i meccanismi sottostanti. Il nostro approccio combina il meglio di due mondi: le equazioni differenziali forniscono le “leggi” biologiche che governano il sistema; le reti neurali imparano dai dati individuali per personalizzare le previsioni. Il risultato è un modello che non solo prevede, ma spiega perché prevede quello che prevede.

L’indice di rischio predittivo

Sulla base delle simulazioni e dell’apprendimento automatico, è possibile definire un indice di rischio predittivo R(t) come funzione dei principali parametri dinamici:

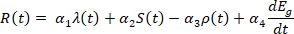
dove i coefficienti α_i sono pesi ottimizzati mediante apprendimento supervisionato. Quando R(t) → 1, indica alta probabilità di transizione degenerativa imminente.

L’andamento di R(t) nel tempo costituisce una curva di rischio personalizzata per ciascun individuo, ottenibile integrando misurazioni longitudinali di neuroimaging e parametri matematici derivati.

Conclusioni e prospettive

Questo studio ha proposto un quadro teorico e computazionale per descrivere i processi neurodegenerativi attraverso strumenti matematici rigorosi. L’approccio adottato ha permesso di formulare una rappresentazione quantitativa del decadimento cerebrale, in cui la perdita sinaptica, la riduzione della plasticità e la disgregazione della connettività funzionale emergono come fenomeni di instabilità dinamica all’interno di un sistema complesso adattivo.

I risultati principali della nostra ricerca includono:

• Formalizzazione del decadimento sinaptico mediante equazione differenziale che integra plasticità e degenerazione
• Descrizione topologica della degenerazione come processo di frammentazione del grafo cerebrale
• Introduzione dell’entropia cerebrale come indice matematico della perdita di organizzazione cognitiva
• Identificazione dei segnali precoci (early warning) mediante critical slowing down
• Framework predittivo ibrido che combina modelli causali e apprendimento automatico

La traduzione di concetti matematici in biomarcatori computazionali offre nuove prospettive per la medicina predittiva. In particolare:

• Le metriche derivate (λ(t), S(t), E_g(t)) possono essere confrontate con dati di neuroimaging e test cognitivi longitudinali
• Il modello può essere integrato in piattaforme di machine learning per previsioni personalizzate
• L’implementazione di digital twin cerebrali consentirà la simulazione individualizzata degli effetti di farmaci e interventi

Le patologie neurodegenerative appaiono, nella prospettiva qui delineata, come fenomeni complessi governati da leggi matematiche che si manifestano nella materia cerebrale. La loro comprensione richiede un dialogo continuo tra modelli formali e osservazioni biologiche.

Il presente lavoro ha voluto dimostrare che tale dialogo è possibile e che la matematica può divenire non solo strumento descrittivo, ma lente predittiva e interpretativa della mente umana.

Attraverso modelli, numeri e reti, possiamo oggi tentare non solo di studiare la degenerazione, ma di prevederla, comprenderla e forse, un giorno, arrestarla.